Main Page

Lecture Notes
Chapter 2

A procedure that maps elements in the represented system into elements in the representing system so that the relationship between the elements in the represented system are maintained in the representing system.

• Allows clear definition of "representation"

Must be testable

Predictive

Testable

Depends on extensiveness of isomorphism between represented and representing systems

• Weigh object
• Scale
• Produces numerical value

Can apply mathematical functions

• e.g., addition, subtraction, greater than, less than, equal to, etc.

• Makes valid use of all the arithmetic operations and relations

• e.g., (X,Y)

• (X1,Y1) + (X2,Y2) = ((X1+X2),(Y1+Y2))

• (X1,Y1) - (X2,Y2) = ((X1-X2),(Y1-Y2))

Latitude

• North/south

• East/west

• Edmonton
  • 54 degrees latitude, 114 degrees longitude
  • (54,114)
• London (England)
  • 51 degrees latitude, 0 degrees longitude
  • (51,0)
• If you travel from Edmonton to London, what is the change in position?
  • New position minus old position
    • (51,0) - (54,114)
    • =((51-54),(0-114))
    • =(-3,-114)
  • 3 degrees of latitude south and 114 degrees of longitude east

Temporal positions and intervals

• Point in time and time between two points in time

• Set of values
  • e.g., December 25
• Single value
  • e.g., Day 359

• "Temporal coordinates"

• Not true vectors
  • Do not represent orthogonal dimensions
• Rules of vector algebra do not apply

• Represented system
• Mapping/correspondence
• Representing system

• Not necessarily simple:simple or complex:complex
• Hierarchical; some representations computed from others

• Not based on complexity
• 1. Is there a correspondence between elements in represented and representing systems?
• 2. Is the correspondence used

Therefore:

• Can't determine nature of representation just by knowing how represented entities map onto representing entities

Representing system must perform operations on entities generated by mapping

Must be a correspondence between operations performed by represented and representing systems

• Determines character of representation

Need behavioural observations

"The best guide to the character of the representations a brain makes is the behaviour the grain generates." (p. 24)

• Learning reveals functional neurology

• Don't infer internal structure; behaviours alone

• Behaviours reveal cognitive processes

• Cross-species comparison reveals functional differences in neurology

• Combine behavioural observations with neurological imaging techniques

• "Brain processes and relations recapitulate world processes and relations."

• Selects representations
• Creates rich isomorphisms between environment and brain systems

• Top down or bottom up?

• Small systems interact to produce unpredictable effects
  • A difficulty for reductionisms
  • Is the synthetic approach any better?

• Not necessarily an error in the representing system
• Representation of uncertainty may be necessary

• Does exist naturally
• Actually, very difficult to truly generate randomness in a representing system
• e.g., Hayes, B. (2001) Randomness as a resource. American Scientist, 89: 300-304.

• Most impoverished form of numerical representation
• Uses "equals" or "identity" operator

• Depends on formal correspondence between systems
• Direct requires formal correspondence

Direct representation

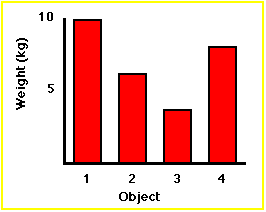
Indirect representation

Object	Weight (kg)
1	10
2	6
3	3
4	8

• Formal characteristics of conscious experience
• Underlying physiological processes

• Environment
• Brain processes

Functions in brain that transform one representation into another

Not interesting

e.g., light passing through lens of eye onto retina

Adaptive

Interesting

Select successful isomorphisms

Isomorphisms are functional in animal's survival (i.e., reproductive success)